Tập hợp Z là một khái niệm toán học đặc biệt, nhưng bạn có biết tập hợp Z là gì không? Tập hợp Z đại diện cho tập hợp tất cả các số nguyên, bao gồm số dương, số âm và số không. Đặc điểm chính của tập hợp Z là có thể sắp xếp từ nhỏ đến lớn và ngược lại, và nó cũng có thể được biểu diễn dưới dạng một đường thẳng số vô hạn.
Tập hợp Z rất quan trọng trong nhiều lĩnh vực toán học và được sử dụng rộng rãi trong các phép toán.. Hãy cùng tìm hiểu chi tiết hơn qua nguoiquangphianam và những thông tin cụ thể trong bài viết sau.
Bạn đang xem: Tập Hợp Z là gì – Số Nguyên và Số Thực
Tập Hợp Z là gì?
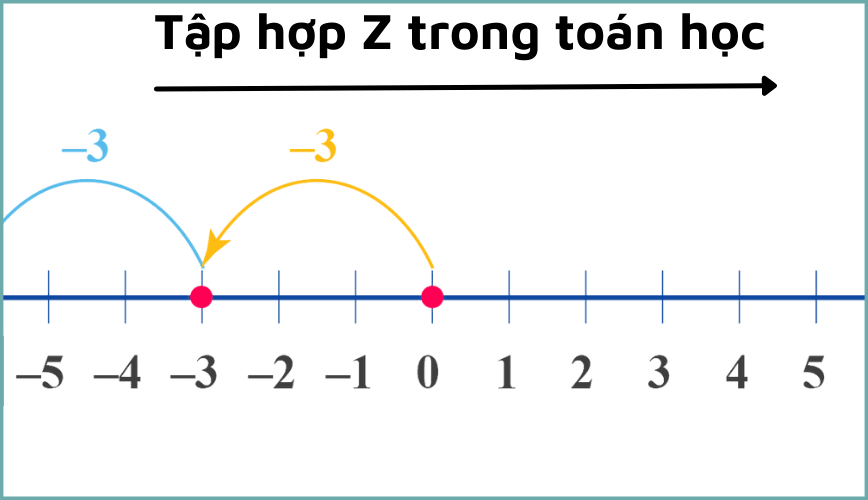
Tập Hợp Z là một khái niệm trong toán học, có nguồn gốc từ ngôn ngữ Hy Lạp “Zahl” có nghĩa là “số”. Tập Hợp Z bao gồm tất cả các số nguyên: từ âm vô cùng, các số nguyên âm, số 0 và các số nguyên dương. Nó được ký hiệu bằng chữ Z và mô tả bằng dấu chấm (.) với mỗi số nguyên.
Ví dụ, Tập Hợp Z = {…, -3, -2, -1, 0, 1, 2, 3, …}. Tập Hợp Z được sử dụng trong nhiều lĩnh vực khác nhau như đại số, số học và lý thuyết số.
Số nguyên là gì?

Xem thêm : Chuyến hành trình từ ác quỷ trở thành thiên thần của Vô Diện
Số nguyên là một khái niệm căn bản trong toán học, gồm có các số nguyên dương, số nguyên âm và số 0. Số 0 được coi là một số đặc biệt nằm giữa hai loại số nguyên dương và nguyên âm.
- Tập hợp số nguyên Z
Tập hợp số nguyên Z là một phần của tập hợp số hữu tỉ Q và số thực R. Nó cũng là tập cha của tập hợp số tự nhiên N. Tập hợp số nguyên Z có hai phần: Z+ và Z-. Z+ bao gồm các số nguyên dương lớn hơn 0, trong khi Z- bao gồm các số nguyên âm nhỏ hơn 0. Số 0 thuộc tập hợp số nguyên Z.
- Tính chất của tập Z
Tập hợp số nguyên Z không có giới hạn số nguyên lớn nhất và nhỏ nhất. Số nguyên trong tập hợp này chỉ có tính tương đối và phụ thuộc vào từng trường hợp cụ thể. Số nguyên dương nhỏ nhất trong tập hợp là 1 và số nguyên âm lớn nhất là -1.
Tập hợp số nguyên Z có vô số tập con hữu hạn, và mỗi tập con này có số nguyên nhỏ nhất và lớn nhất riêng của nó. Bên cạnh đó, không có số nguyên nào nằm giữa hai số nguyên liền kề trong tập hợp này. Nội dung
Các tập hợp số khác

Các tập hợp số |
Nội dung |
| Số tự nhiên N | Tập hợp các số tự nhiên N. N gồm các số 0, 1, 2, 3, … và được sử dụng để đếm và lưu trữ thông tin. |
| Số hữu tỉ Q | Tập hợp các số hữu tỉ được gọi là Q. Nó bao gồm các số có thể được biểu diễn dưới dạng phân số, trong đó a và b là số nguyên và b khác 0. Mỗi số hữu tỉ có thể có nhiều cách biểu diễn khác nhau và có thể là số thập phân lặp hoặc không lặp. |
| Số vô tỉ I | Tập hợp các số vô tỉ được gọi là I. Đây là tập hợp các số thực không thể biểu diễn dưới dạng phân số. Số vô tỉ được sử dụng trong nhiều lĩnh vực như điện tử, vật lý và toán học ứng dụng. |
| Số thực R | Tập hợp các số thực được gọi là R. Nó bao gồm số tự nhiên, số nguyên, số hữu tỉ và số vô tỉ. Số thực là tập hợp lớn nhất và bao gồm số dương và số âm. Trừ số 0, tất cả các số thực khác có thể là số âm hoặc số dương. |
| Số phức C | Tập hợp các số phức được gọi là C. Số phức có dạng a + bi, trong đó a và b là số thực và i là đơn vị ảo. Số phức được sử dụng trong nhiều lĩnh vực như điện tử, cơ học và toán học ứng dụng. |
FAQ – Giải đáp những thắc mắc về tập Hợp Z là gì
1.Tập Hợp Z là gì?
Xem thêm : Chất C2H4 Là Chất Gì? Tính Chất Và Ứng Dụng Của Etilen Trong Thực Tế Như Thế Nào?
Z là tập hợp các số nguyên, bao gồm số dương, số âm và số không.
2. Tập hợp Z quan trọng trong toán học, vì sao?
Tập hợp Z quan trọng trong toán học vì nó giúp chúng ta hiểu và làm việc với các số nguyên, bao gồm cả số âm và số không. Tập hợp Z là cơ sở cho nhiều phép toán khác nhau như cộng, trừ, nhân và chia. Nó cũng đóng vai trò quan trọng trong lĩnh vực số học và lý thuyết đồ thị.
3. Có thể đưa ra ví dụ về việc sử dụng tập hợp Z trong cuộc sống hàng ngày được không?
Tất nhiên! Một ví dụ phổ biến là khi chúng ta xử lý tiền tệ. Khi bạn mua sắm và thanh toán cho một mặt hàng, số tiền bạn trả là một số nguyên thuộc tập hợp Z. Lúc này, tập hợp Z giúp chúng ta tính toán và xác định các giao dịch tiền tệ một cách chính xác.

Lời kết
Trên đây chúng ta đã cùng tìm hiểu về tập hợp Z là gì? Và ý nghĩa của nó. Việc hiểu rõ về tập hợp Z không chỉ giúp chúng ta nắm vững các kiến thức căn bản về số học mà còn giúp chúng ta áp dụng thành công vào thực tế.
Hy vọng qua bài viết, bạn đã hiểu rõ hơn về tập hợp Z là gì? Và nhận thức được tầm quan trọng của nó trong cuộc sống hàng ngày cũng như trong lĩnh vực học tập và công việc của bạn. Chúng ta hãy tiếp tục khám phá những khái niệm thú vị khác và áp dụng chúng vào cuộc sống thực tế nhé. nguoiquangphianam Cảm ơn bạn đọc
Nguồn: https://nguoiquangphianam.com
Danh mục: Tin Tức